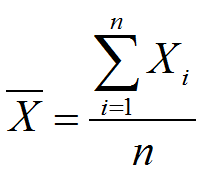What do you mean? How Grades Abuse Statistics

This is the first post in our series exploring why grades suck. It exposes one of the most egregious, and ironically unexamined shortcomings of grades, which is at the heart of how they are calculated–the use of the arithmetic mean, i.e. the average.

Most grades are calculated as a sum or average of some set of scores.  Two relevant questions to ask are:

1. What is the source of those sums or averages?
2. Is the interpretation of those averages statistically sound?

Let’s actually start with the second question first.  Statistics is a field of analysis which seeks to use the properties of numbers and mathematics to make justifiable and accurate descriptions and predictions about phenomena in the world.  We typically think of the Mediterranean as a sunny and warm place.  However if you were thinking of escaping a cold Virginia winter, you may be surprised to learn that the average January temperature in Malta is only 50-60°F.  Here we’ve used the arithmetic mean, i.e. the average, a statistical analytical procedure, to interpret weather phenomena.  Your likely conclusion in this case is that if you do plan to go to Malta in January, the interpretation of the statistic is pretty clear: you’d better take a jacket.

Let’s try the same interpretive exercise with grades.  Let’s say that a student, Otis, got an 87 on an assignment.  Here are some plausible interpretations.  In each, pay close attention to how you feel towards Otis.

• Otis, normally an A student, was feeling sick and didn’t perform so well
• Otis, normally a C student, really studied hard and outperformed his usual scores
• Since the class average was 96.42, Otis fell well below his peers’ performance
• Since the class average was 42.96, Otis did extremely well on this assignment
• Otis’ paper was on top of the stack when the teacher began grading so evaluated it more strictly than later papers
• Otis’ paper was on the bottom of the stack, and the teacher, being tired by this point, graded leniently
• The teacher had a mistake on the key used to score the assignment
• Otis has undiagnosed test anxiety disorder, which means he routinely scores below his potential
• This particular teacher really likes/dislikes Otis
• This is a particularly rigorous/unchallenging course, school, etc.
• etc., etc., etc.

I’m sure that many more different scenarios could be developed.  Regardless, based on the number alone, without understanding the context, it is nearly impossible to interpret.  “But wait!” you say, “Wouldn’t such difficulties in interpretation be alleviated if we had an average of all of Otis’ scores for a whole semester?”  Answer the question for yourself by imagining that instead of one assignment, Otis got an 87 for the semester, or a 2.96 GPA for his entire time in college.  Can you not come up with an equally large number of plausible interpretations of such scores?  The problem lies in a misapplication of statistical procedure.  Misapplication of statistics results in the inability to make a reliably meaningful interpretation.

What is different about the average temperature example and the average grade example is the source of the underlying data used to calculate the statistic.  Average temperature is based on quantitative data whereas grades are based on qualitative  data.  “But,” you ask,”isn’t an 87, or a 2.96, a number? Don’t numbers represent quantity by their very nature?” Nope. In the case of grades, an 87 is higher than an 86 and lower than an 88, but these are just indicators of relative quality.

I’ll illustrate this more clearly with another example.  Take the scale below that might be commonly be seen on a customer satisfaction survey in response to a question, such as, “How satisfied were you with your server, today?”

Now it’s clear that “satisfied” is a higher ranking than “dissatisfied,” and while it’s clearly possible (and actually common) to assign each of these rankings a number, say from 0 to 4, does a ranking of 4 (extremely satisfied) really mean that a customer is “twice as satisfied” as one that gave the server a 2 (neither satisfied nor dissatisfied).  Is a customer who gave the server a 3 three times as satisfied as a customer who gave the same server a 1?  I don’t think so.  And even if this were the case, how would we make a meaningful interpretation of these values?  Can you not come up with a nearly endless list of reasons as to why a particular server/customer interaction might have yielded those scores?  Getting back to grades, is a score of 80 twice as good as a 40?  Is 100 twice as good as 50? 60 twice as good as 30?  A 4.0 twice as good as 2.0? Did the person who scored the higher score learn twice as much? Not likely. And it’s because grades don’t represent quantity but quality.

We could dive more deeply into the source of the 87, but hopefully the point is made.  Consult a textbook on statistical analysis and it will tell you that the arithmetic mean is not applicable to analysis of qualitative data (except in very specific circumstances which are not really relevant and beyond the scope of this post).  Grades are clearly qualitative, not quantitative, and therefore should not be analyzed with averages lest they be susceptible to misinterpretation.

Incidentally, I find it painfully ironic that nearly all statistics class grades are determined using averages.  You should note that in ISAT, Dr. Radziwill does NOT do this.  She uses a points accumulation system, and in fact, the points accumulation system in this class is patterned after hers.

In another post I’ll explore a really fascinating 2000 paper by Vickers that shows that because of the inconsistencies in GPA calculations across different institutions, it is logically impossible to rank students using GPA.

What does this mean?

The bottom line is that nobody really knows, for sure, what any particular grade means. Because of the abuse of statistics grades have no reliably meaningful interpretation. And yet, grades and GPA are used to determine:

• If a student passes a course
• If someone should get into college or graduate school
• Who qualifies for scholarships
• Who can get a job interview
• How “effective” any number of pedagogical interventions are

In our hearts, we know that grades don’t really define us. We sense it every time we get feedback that is in conflict with our gut sense of who we are or what we know. Now you know one reason why.